Gamma matrices

The gamma matrix basis used is:

$$\begin{array}{ccccccc} \gamma_1 &=& \left(\begin{array}{rrr... ...&0 \end{array}\right) &=& \sigma_1\!\otimes\!1\\ \end{array}$$

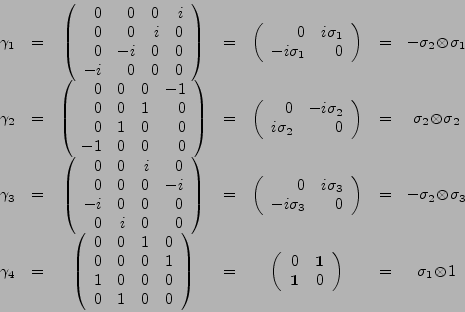
This is a chiral basis and is the same basis currently used in QDP++.

For functions that multiply by a gamma matrix the gamma matrix is specified by an integer between 0 and 15. The mapping from the integer to a general gamma matrix is:

$$\Gamma(n) = \gamma_1^{n_0} \gamma_2^{n_1} \gamma_3^{n_2} \gamma_4^{n_3}$$

where the binary representation of n is n₃ n₂ n₁ n₀.